RAID is a popular choice to increase storage performance and redundancy for systems with multiple disks. Especially enterprise and professional storage settings prefer RAID levels 5 and 6, with RAID 5 being a popular choice for low compute overhead and minimal reduced storage space.
How RAID 5 works
On an abstract level, RAID level 5 combines the techniques of striping and parity data. Using parity data enables the disk array to survive a single failing disk (no matter which disk fails). The missing data can be recomputed using the parity data, as long as all other disks are still operational. For any number of disks in the RAID 5 array, only a single disk worth of space will be lost for this parity data.
The wording "one disk is used for parity" may be confusing: RAID 5 requires all disks in the array to be the same size. If the disks have different capacities, the smallest disk in the array will be used for disk size, and all other disks can only use as much capacity as the smallest disk offers. As an example, if you combine 3 100TB disks and one 1TB disk into RAID 5 array, then RAID 5 will treat all disks as 1TB disks (making the remaining 99TB on the larger disks unusable).
Striping
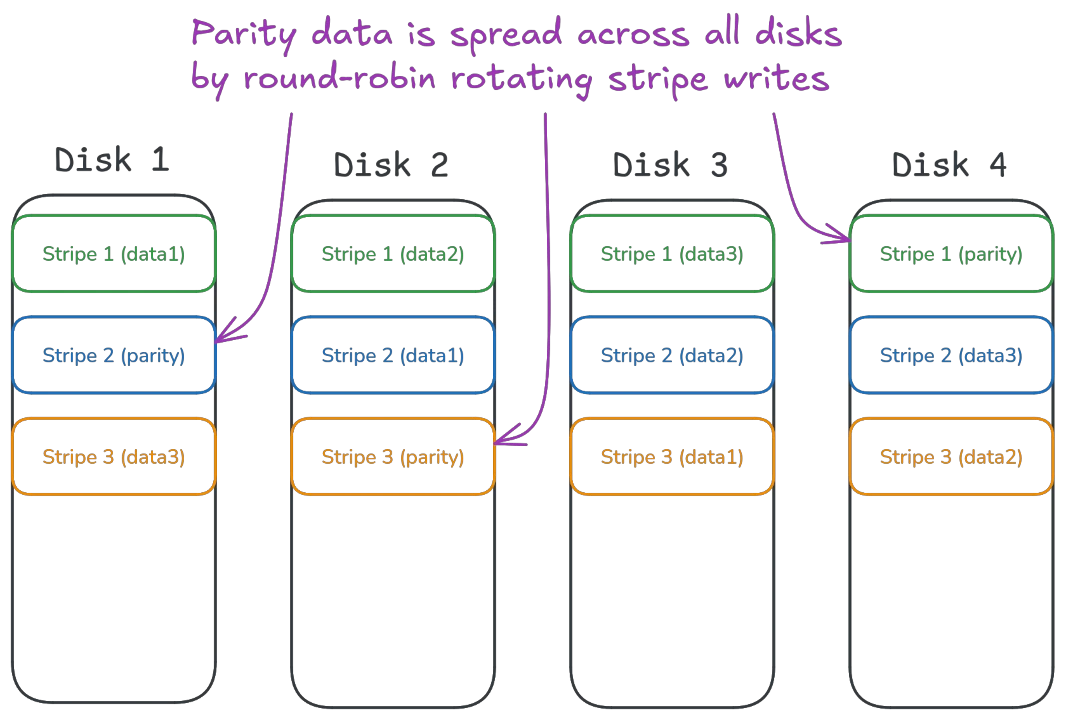
One important aspect of RAID 5 is its use of striping: Data that is written to the array is split into smaller pieces called "stripes". Stripes are further split into chunks (one per disk), and parity data is computed from these chunks. Then the stripe's chunks and the parity data are written to the disks in a rotating fashion, to ensure the parity chunks are spread evenly among all disks.
Striping increases the overall performance of the RAID 5 array, because data belonging to a stripe can be simultaneously read from all disks in the array (except one, which holds the parity data for the stripe). Effectively, the array allows programs to use the combined read and write bandwidth of all disks at once, instead of relying on any one disk's abilities.
How parity is calculated
The parity data needed to recover missing stripe chunks is computed using the exclusive or (XOR) operation. XOR works by comparing the bits in binary data, producing a 0 if the bits are equal (both are 0 or both are 1), or a 1 if they are different (one is 0 and the other is 1).
The parity data is computed by XORing the data of all chunks in a stripe, then adding the resulting parity data to the stripe.
Using the XOR operation guarantees that the parity chunk is the same size as any other data chunk in the stripe, no matter how many data chunks are actually in the stripe.
Recovering missing data with parity
When a disk fails, the missing data can be computed no matter which chunk of the stripe is missing. If the parity chunk is missing, XORing the data chunks would reproduce the parity data. If a data chunk is missing, the missing data can be replaced with the parity data, then XORing all chunks will produce the missing data.
Let's look at this with an example stripe:
10101001 | data1
11010000 | data2
00100101 | data3
01011100 | parity (data1 XOR data2 XOR data3) Assuming any disk fails, its data chunk can be recomputed by XORing the data chunks and replacing the missing data chunk with the parity chunk:
data1 = parity XOR data2 XOR data3
data2 = data1 XOR parity XOR data3
data3 = data1 XOR data2 XOR parityAs long as only one chunk (disk) is missing, any missing data can be recomputed, no matter which chunk is missing.